Display the solution version in your web part9 min read

Introduction

Displaying the version number in your web part can make it easy to quickly identify areas in your SharePoint tenant(s) where you have not updated your web part solution.

If you’re ever trie to handle a helpdesk call with a site owner who was experiencing problems with a web part you wrote, and you could have sworn you fixed the issue the user is describing — only to find out that they have an older version of your web part — you’ll know what I’m talking about.

On the March 26th SharePoint Framework Community Call, Bo George demoed a very cool Q&A solution for SharePoint written in SPFx. During his demo, he demonstrated that he added the web part version in the property pane.

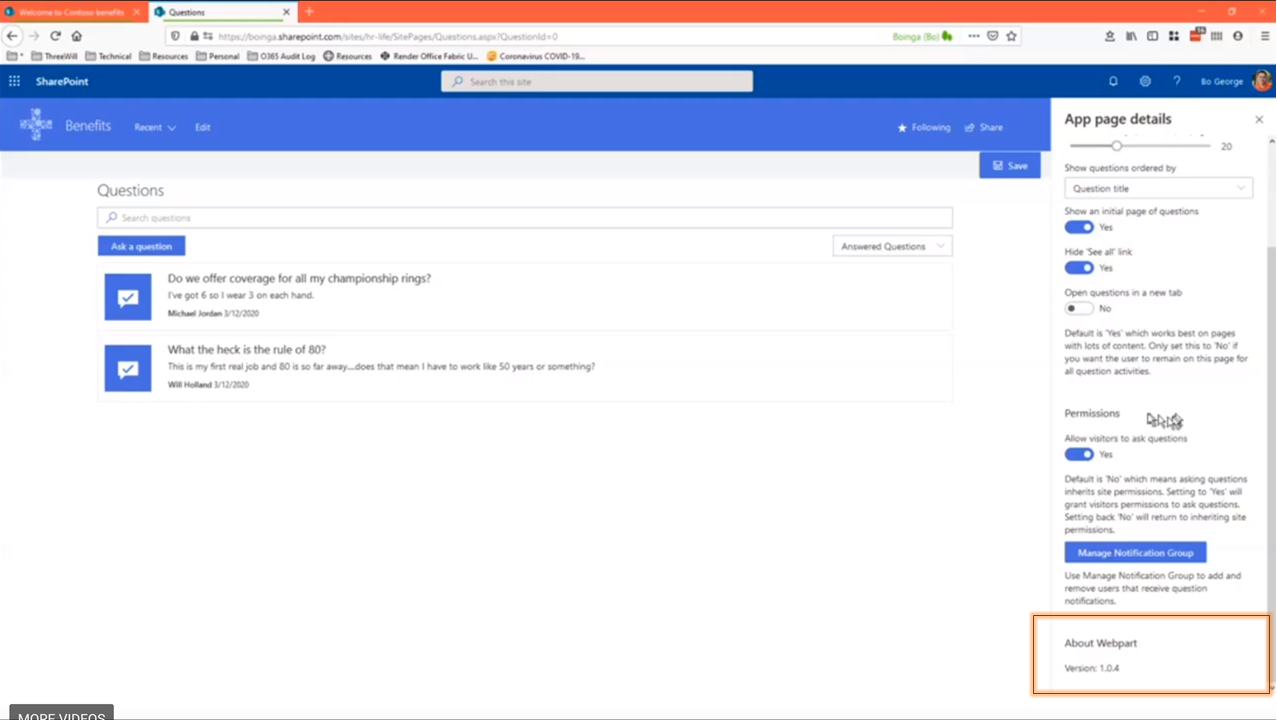
Unfortunately, Bo didn’t get to share his code, but it is something that I also like to do in my production web parts.

In this article, I’ll share my approach for showing the solution version in your web part.

I’m sure Bo’s code is much cooler than mine, but this is the method I use.

Where is the version number stored?

NodeJS projects have a version number which is stored in your project’s package.json. It follows the semantic versioning guidelines, which consists of a major, minor, and patch version.

SharePoint solutions, however, use a different versioning scheme, which consists of a major, minor, patch, and a revision number.

Stefan Bauer does a great job at explaining the differences between the two types of versioning.

The SharePoint solution version that SharePoint displays when you show Details about a web part is stored in src\package-solution.json in your project. This is an example of the version format that SharePoint uses:

Syncing the NodeJS package version with the solution version

I like to keep the NodeJS version in sync with the SharePoint solution. But I really dislike copying the version numbers manually.

I may have mentioned once or twice that I’m the world’s laziest developer — if I can avoid to do anything more than once, I try to avoid it.

Fortunately Stefan also has a great solution to automatically synchronize the NodeJs package version to your SharePoint package solution version every time you build the solution.

If you use the PnP SPFx Yeoman generator, there is already a gulp task that will execute every time you run npm version.

If you use the regular SPFx Yeoman generator — not the PnP one — you can achieve the same thing by adding a custom gulp task written by Stefan.

You can do the same thing by following these steps:

1. In your SPFx solution, edit your gulpfile.js
2. Find the following line:

   build.initialize(require('gulp'));

3. Insert the following code before the line you found in step 2.

   // This section is inspired by Stefan Bauer's article at https://n8d.at/how-to-version-new-sharepoint-framework-projects/
   // Stefan rocks!
   let syncVersionsSubtask = build.subTask('version-sync', function (gulp, buildOptions, done) {
   this.log('Synching versions');
   
   // import gulp utilits to write error messages
   const gutil = require('gulp-util');
   
   // import file system utilities form nodeJS
   const fs = require('fs');
   
   // read package.json
   var pkgConfig = require('./package.json');
   
   // read configuration of web part solution file
   var pkgSolution = require('./config/package-solution.json');
   
   // log old version
   this.log('package-solution.json version:\t' + pkgSolution.solution.version);
   
   // Generate new MS compliant version number
   var newVersionNumber = pkgConfig.version.split('-')[0] + '.0';
   
   if (pkgSolution.solution.version !== newVersionNumber) {
   // assign newly generated version number to web part version
   pkgSolution.solution.version = newVersionNumber;
   
   // log new version
   this.log('New package-solution.json version:\t' + pkgSolution.solution.version);
   
   // write changed package-solution file
    fs.writeFile('./config/package-solution.json', JSON.stringify(pkgSolution, null, 4), function (err, result) {
           if (err) this.log('error', err);
       });
   }
   else {
   this.log('package-solution.json version is up-to-date');
   }
   
   done();
   }); 
   let syncVersionTask = build.task('version-sync', syncVersionsSubtask);
   build.rig.addPreBuildTask(syncVersionTask);

That’s it. Now, next time you run a gulp build, the Stefan’s gulp task will make sure both versions are in sync.

Changing the version number

To change the package version of your solution, you can simply edit the package.json version.

But npm has a command to easily change your package version. You can call any of the following commands from your SPFx solution folder:

npm version major
npm version minor
npm version patch

…to change the major, minor, and patch version — respectively — in your package.json.

When to change major, minor, and patch version

I often see two extremes: either developers leave their solution versions at 1.0.0 no matter how many times they change their code, or they semi-randonmly change the version number every time they change their code.

Luckily, semantic versioning (or semver) provide guidelines on how to change your package versions.

You should pretty much always start at version 1.0.0, and increase the major, minor, and patch versions depending on the types of changes you made.

The following table shows when you should call which npm version command, depending on the types of changes you’re making to your solution:

Type of change	Stage	Versioning rule	Example version	NPM command
First release	New solution	Start with 1.0.0	1.0.0	npm version major
Backward compatible bug fixes	Patch release	Increment the third digit	1.0.1	npm version patch
Backward compatible new features	Minor release	Increment the middle digit and reset last digit to zero	1.1.0	npm version minor
Changes that break backward compatibility	Major release	Increment the first digit and reset middle and last digits to zero	2.0.0	npm version major

Using the manifest version

Probably the easiest way to display the version number is to use the version property of the web part’s manifest which is available in the web part’s context, for example:

const version: string = `Version: ${this.context.manifest.version}`;

Unfortunately, the version number that comes from the manifest is a 3-digit version (major.minor.patch), whereas the version number in your SharePoint solution is a 4-digit version.

Now, that’s perfectly fine if you don’t use the 4th digit (the revision) in your SharePoint solution version numbers, or if — like me — you sync your package.json version with the package-solution.json. You can simply add an extra .0 at the end of the version from this.context.manifest.version.

If you want to get the 4-digit version number, however, it gets a little more complicated…

Importing the version number using a static import

To get the 4-digit version from your SharePoint solution, you’ll need to import the version number that’s found in the package-solution.json in your code.

Your first instinct might be to simply add an import statement to your code and point to your project’s config/package-solution.json, like this:

// Static import
import * as packageSolution from '../../../config/package-solution.json';

But — depending on the version of TypeScript you’re using –you’ll likely get a nasty error:

Error - [tsc] src/webparts/versionDisplay/VersionDisplayWebPart.ts(21,34): error TS2732: Cannot find module '../../../config/package-solution.json'. Consider using '--resolveJsonModule' to import module with '.json' extension

You could add "resolveJsonModule": true to your solution’s tsconfig.json, but I have found that it doesn’t consistently work — depending on which version of TypeScript you’re using.

Instead, I use the following steps:

1. In your project’s src folder, add a file called typings.d.ts
2. Paste the following code to your newly created file:

   declare module "*.json" {
   const value: any;
   export default value;
   }

3. In your code add a static import to your package-solution.json (you may have to adjust the path to the file depending on where in your code you’re adding your import)

   // Static import
   import * as packageSolution from '../../../config/package-solution.json';

4. When you want to display the version number, use the following code:

   (<any>packageSolution).solution.version

Importing the version using require

You can also use a require statement, by following these steps:

1. In your code, where you want to insert the version number, insert this code:

   // Import package version
   const packageSolution: any = require("../../../config/package-solution.json");

   (Again, the path to your package-solution.json may vary depending on where you’re adding the code)

2. When ready to show the version number, you can simply use:

   packageSolution.solution.version

Displaying the version number in the property pane

To display the version number, I like to use the PropertyPaneWebPartInformation control from the @pnp/spfx-property-controls library.

To do so, follow these steps:

1. Import the @pnp/spfx-property-controls-library package in your solution by entering the following command in your command-line:

   npm install @pnp/spfx-property-controls --save --save-exact

2. Add the following import to your web part class:

   // Used to display version information
   import { PropertyPaneWebPartInformation } from '@pnp/spfx-property-controls/lib/PropertyPaneWebPartInformation';

3. In your web part’s getPropertyPaneConfiguration method, add the following code inside the groups array:

   {
   groupName: "About",
   groupFields: [
       PropertyPaneWebPartInformation({
           description: "Version: " + (<any>packageSolution).solution.version,
           key: 'webPartInfoId'
       })
   ]
   }

The full code for my getPropertyPaneConfiguration looks as follows:

protected getPropertyPaneConfiguration(): IPropertyPaneConfiguration {
    return {
      pages: [
        {
          header: {
            description: "This web part displays the current version of the solution"
          },
          groups: [
            {
              groupName: "About",
              groupFields: [
                PropertyPaneWebPartInformation({
                  description: "Version: " + (<any>packageSolution).solution.version,
                  key: 'webPartInfoId'
                }),
              ]
            }
          ]
        }
      ]
    };
  }

Note that I didn’t localize the code for simplicity, but please use localized resources instead of hard-coded text.

When you’re done, your web part’s property pane should display the current version number:

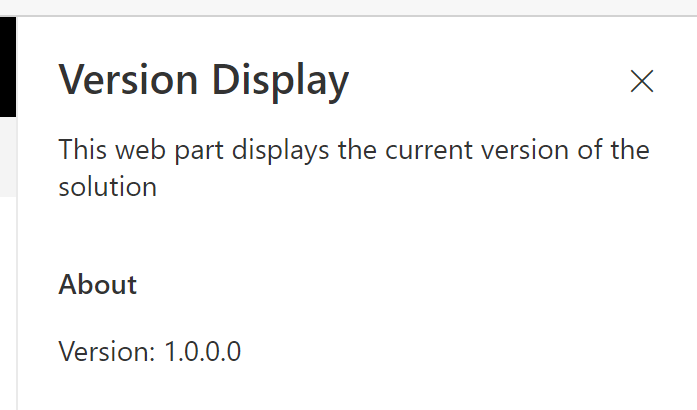
Conclusion

I know it was a very long explanation for such a simple concept, but our goal was to make sure that we never have to copy the version number of your web part manually.

We also learned how to properly version solutions along the way.

Thanks to Bo George for the inspiration to write this article, and Stefan Bauer for writing a custom gulp task that I use in every one of production SPFx solutions.

You can find the code for this solution in my .

I hope this helps?

Update

• April 1, 2020: After joking with Stefan Bauer that this should be a standard feature in the PnP SPFx Yeoman generator, he pointed out that it is already a feature. I updated my article accordingly.
• April 1, 2020: Ohmygod ohmygod ohmygod! read my blog and reached out to me to point out that I should tell people how to use the this.context.manifest.version before importing the package-solution.json. She’s absolutely right, plus I’m such a big fan of her work. I’ve updated my article accordingly.
• March 31, 2020: suggested that it might be a good idea to add a link to launch the web part maintenance mode, and I really like it. You just need to append ?maintenancemode=true to the page URL to turn the page into maintenance mode. Great idea!

Photo credits

Photo by Nick Hillier on Unsplash